DB Index에서 사용되는 B-Tree (데이터 삭제)

데이터 삭제는 아래 2가지만을 신경쓰면 된다.
1. 항상 leaf 노드에서 삭제가 발생.( internal node의 삭제 시에도 항상 leaf 노드가 삭제된다. 한참 아래에 internal node 삭제에 대한 설명이 있음)
2. 삭제 후, 해당 노드의 key수가 최소 key 수 보다 적어졌으면 재조정한다.
2-a) 형제 노드들 중, key의 수가 최소 key 개수보다 많으면 그 key를 가져와서 재조정한다.
2-a-1) 왼쪽 형제가 더 여유가 있으면...(원래 일반적으로 왼쪽 형제의 지원을 우선적으로 받는다.)
->동생의 가장 큰 KEY를 부모 노드에게 올려 주고
-> 부모 노드에 있던 KEY를 나에게 내려 준다,
2-b) 형제 노드의 도움으로도 해결이 되지 않으면, 그 다음에는 부모 노드의 key값을 가지고 와서 형제 노드와 합친다(합칠 때는 항상 오른쪽 노드를 왼쪽 노드로 합친다.)
2-b-1) 왼쪽 형제에게 여유가 없고, 오른쪽 형제에게 여유가 있다면...
-> 오른쪽 형제의 가장 작은 KEY를 부모에게 올려주고,
-> 부모 노드에 원래 있던 KEY를 나에게 내려준다.
2-c) 만약 2-b)를 수행하는 과정에서 부모 노드의 key 개수가 또 최소 key 개수보다 작아지면 똑같은 방식으로 다시 재조정을 한다.
3. 형제 노드에서 재조정을 위한 KEY의 지원이 불가하면, 부모 노드의 지원을 받아 재조정을 한다.
( 최소 key 수 = (M/2) - 1 , B-Tree의 삭제에서는 최소 key 수가 핵심 포인트! )
( 위 트리는 3차 트리이므로 최소 key의 수는 1 개이다.)
삭제 시, 형제 노드들의 지원을 받아 재조정을 하는 경우
1] 6 삭제

2] 5삭제

5가 사라진 노드의 key의 개수가 1개 보다 적어졌으므로, 재조정을 해야 한다.
먼저 형제 노드들 [1,2]과 [8,9]들이 최소 key 개수보다 많으면, 그 key값을 들고 와 보려고 시도를 한다.
( 보통, key 값들이 작은 형제 노드들로부터 key 값을 들고 온다. )
두 형제 노드들은 최소 key 개수를 모두 만족하기에 재조정이 간단할 것 같다.
그러나 아래를 살펴 보자

만약 [1,2] 노드에서 key값을 들고 오게 되버리면, 3차 B-Tree의 key 값의 대소 관계가 깨져 버린다.
예를 들어, [1,2]에서 2를 들고 오게 되면, [1] -> [3] -> [2] ->[7]->[8,9]가 되버린다.
고로, 부모 노드로 부터 key값을 들고 오는 방식을 채택해야 한다.

3이 자식 노드로 내려 가고, 그 자리를 [1,2] 의 2를 승진시키므로써, 대소 관계도 충족시키고 B-Tree의 재조정도 완성이 되
었다.

삭제 시, 부모의 지원을 받아 재조정을 하는 경우
3] 7 삭제
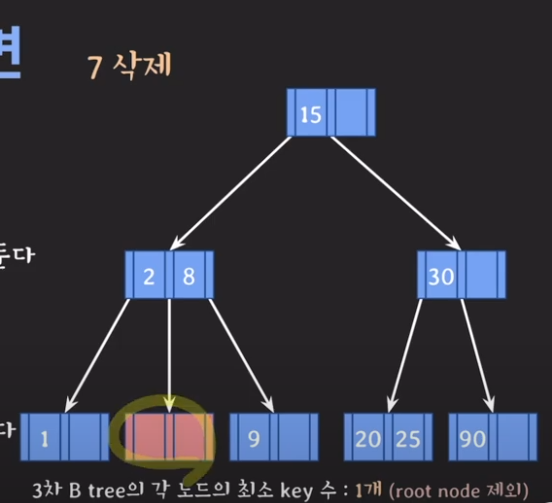
7을 삭제 후, 형제 노드들의 지원을 받아 재조정을 하려고 봤는데,
형제 노드들도 모두 지원해줄 KEY가 없다.
고로, 이제는 부모 노드의 지원을 받아서 형제 노드와 합치는 방식으로 재조정을 해야 한다.


여기에서 원래 형제 노드(빨간색 노드)와 합쳐야 하는데, 아무 KEY값이 없으므로, 빨간색 노드는 없애 준다.

8을 왼쪽으로 이동을 시키면서, 파란색 노드를 가리키는 포인터 값도 젤 오른쪽에서 중간으로 옮긴다.
4] 2삭제
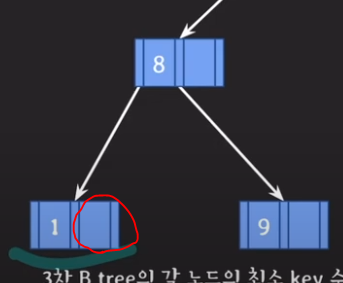
5] 1삭제

형제 노드에게 지원을 받을 수가 없으므로, 부모 노드의 8을 가져와서 형제 노드 9와 합친다.
( 형제 노드를 합칠 때는 항상 오른쪽 노드를 왼쪽 노드로 합친다.)

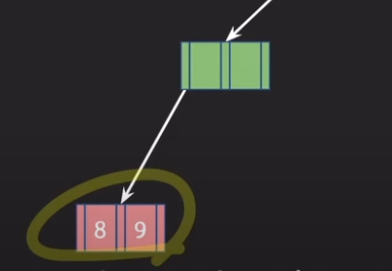
근데, 부모 노드에서 이제는 재조정이 필요하다.
고로, 부모 노드의 형제 노드로부터 지원을 받을 수 있는지 보자!
형제 노드에도 KEY의 개수에 여유가 없다.
고로, 부모 노드의 지원을 받아서, 형제 노드를 합쳐야 한다.
여기서부터는 부모 노드의 KEY 개수가 최소KEY개수보다 적을 때의 재조정에 대해 살펴보자!
삭제 시, 부모 노드에게 재조정이 필요해진 경우!




포인터 값의 위치도 이동시켜 준다.

internal node 데이터 삭제
