아래에 이진 탐색 트리에 대한 간단한 개요가 있다.

이진 탐색 트리는 최대 2 개의 자식 노드를 가질 수가 있다.
그러나 만약 자식 노드의 개수를 3개로 늘리면서, 이진 탐색 트리와 같은 동작 방식으로 데이터를 삽입,조희,삭제를 해주기
위해서는 어떻게 하면 될까???

왼쪽의 BST의 왼쪽 서브 트리의 모든 노드는 50보다 작고, 오른쪽 서브 트리의 모든 노드는 50보다 크다.
오른쪽의 자녀 노드가 3개인 경우에도 이와 같은 규칙성을 가지게 해보자.
일단 자식 노드가 3개이므로, 각 노드의 부모 노드와의 대소관계는 BST가 2개였던 거와는 달리, 3개가 된다.
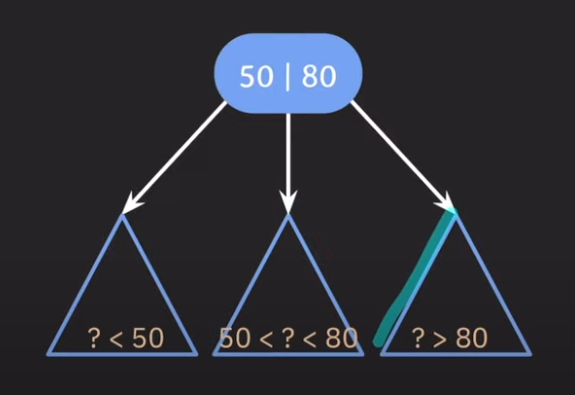
즉, 왼쪽 자식 노드부터 아래와 같이 정의가 된다. ( 참고로, 이때에는 부모 노드가 2개 있어야 한다 )
1] SubTree < k1 : 왼쪽 서브 트리의 모든 노드는 k1보다 작다.
2] k1 < SubTree < k2 : 가운데 서브 트리는 k1보다는 크고, k2보다는 작다.
3] k2 < SubTree : 오른쪽 서브 트리의 모든 노드는 k2보다 크다.
( 부모노드의 개수 = 자식 노드의 개수 -1 )

필요에 따라 자녀 노드를 3개 이상으로 늘려야 할 때, 위와 같이 트리를 만들어서 BST와 비슷한 방식으로 데이터를 삽입,
조회, 삭제를 할 수가 있다. ( 이러한 점에서 B-Tree를 BST의 일반화된 Tree라고도 부른다 )
이러한 형태로 동작하는 트리를 B-Tree라고 한다.

B-Tree의 주요 4가지 파라미터(주로, 각 노드의 key의 갯수와 자녀 노드의 갯수에 대한 것임)

B-Tree 노드의 key의 개수와 자녀 수의 관계(주로, 각 노드의 key의 갯수와 자녀 노드의 갯수에 대한 것임)


B-Tree 데이터 삽입
B-Tree 데이터 삽입 시, 아래 2가지만을 기억하면 동작 방식을 이해하는 데 문제가 없다.
1. 항상 leaf 노드에 key값을 추가를 한다.
2. 삽입 시도 시, 노드가 넘치면(최대 key 개수를 넘으면) 가운데 key(Median Key)를 기준으로, 좌우 key들을 분할시키고,
가운데 key(Median Key)는 승진시킨다.
B-Tree 데이터 삽입 예시

일단, 최대 자녀노드의 갯수가 3개인 3차 B-Tree로 예시를 들거다.
( 3차 -> 최대 자녀 노드 3개 -> 각 노드에 들어가는 key값이 최대 2개 )
1] 1과 15를 삽입을 해 보자.

항상 leaf 노드에 key값을 추가한다.
오름차순으로 잘 정렬되어 있다.
2] 2를 추가하자

key값은 항상 leaf에 추가를 한다.
근데 최대 key값의 개수는 2개인데, 현재 3개의 key값이 들어가 있으므로, 노드가 넘치게 되었다.
노드가 넘치면 가운데 key(Median key)인 2를 기준으로 좌우key, 즉 1(좌)과 15(우)를 분할하고,
가운데 key 2를 부모 노드로 승진을 시킨다. 그 결과는 아래와 같다.

3] 5를 추가하자

추가는 항상 leaf 노드에 해야 한다. key 값 5를 root 노드부터 대소 관계를 비교하여 5가 들어가야 할 leaf 노드를 찾는다.
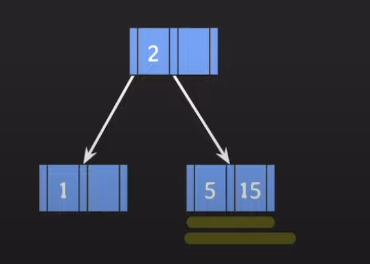
5가 들어갈 leaf 노드를 찾아서, 오름차순으로 잘 정렬하여 삽입을 하면 된다.
3] 30 추가
50이 들어갈 leaf 노드를 찾아서 삽입을 한다.
그러나 노드가 넘치기 때문ㅇ, 가운데 key 15를 부모 노드로 승진시키고, 5(좌측 key)와 30(우측 key)를 분할 시킨다.


4] 이후에 90이 추가됐다고 치고, 20을 추가해보자!

20이 추가가 되었다.
그러나 노드가 넘치기 때문에 분할 및 승진을 시켜야 하며 그 결과가 아래의 그림이다.

여기서 부모 노드도 넘치는 상황이 발생을 하였다.
노드가 넘치기 때문에 똑같이 분할 및 승진을 시켜야 한다.
그러나 여기서는 약간 특이한 점이 있다.
바로 자식 노드가 4개라는 것이다. 현재 우리는 3차 B-Tree를 만들고 있기에 자식 노드가 4개이면 안된다.
고로 아래와 같이 분할 및 승진을 시킨다.


5] 7,9 추가!

6] 8, 10 추가

7] 50,70추가

8] 60 ,40추가

참고로, B-Tree 특징 중 1개로서
모든 leaf 노드들은 같은 레벨에 있다 라는 것이다. 이것이 의미하는 바는 아래와 같다.
-> balanced tree : BST는 편향 트리인 경우, 최악의 경우 0(N)의 시간 복잡도를 가지지만, B-Tree는 밸런스가 잡혀 있기에
최악의 경우에도 O(logN)의 시간 복잡도를 가진다.
'CS 과목(CS科目) > 자료 구조(Data Structure)' 카테고리의 다른 글
| Priority Queue와 Heap의 차이점 (0) | 2023.03.30 |
|---|---|
| DB Index에서 사용되는 B-Tree (데이터 삭제) (0) | 2023.03.10 |
| Deque(덱) (0) | 2023.01.20 |
| 원형 큐(Circular Queue)를 사용하는 이유!!! (0) | 2023.01.15 |
| Stack, Queue, List, set 등의 자료구조 사용 시 주의 사항 (0) | 2023.01.13 |


