(아래의 글을 읽기 전에, MSE랑 Cross-Entropy 설명 시, Activation Function을 모두 Sigmoid 함수로 가정하여 설명을 하고 있다)
MSE(Mean Square Error)
정답 레이블이 INDEX=[0,1] 중 0인 상황에서 예측값(o)이 각각 [0.7503(idx=0), 0.9971(idx=1)] 나온 두 경우를 생각해보자.
(위에서도 언급했듯이, sigmoid 함수를 가정하여 설명하고 있으므로, idx=0과 idx=1은 동시에 나오는 값이 아니다.)
(참고로, sigmoid 함수는 Binary Classification 등에서 주로 사용된다)
후자(0.9971)가 조금 더 큰 에러가 발생했으므로, 더 큰 그레디언트 값을 이용하여 가중치(weight)를 갱신시켜 주어야 할
것이다.
(idx=0의 확률의 오차는 0.24이고, idx=1의 확률의 오차는 0.9971이다. idx=1은 정답 레이블이 아니므로 확률이 0이 여야
하는데, 1에 가까운 0.9971이 나왔다. 고로, 0에 수렴하도록 가중치 값을 크게 업데이트 시켜야 한다)
But...... 결과적으로는 그렇게 되지 못하는 경우가 있다.
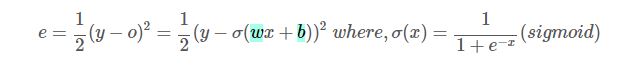
MSE 식에서 각각 파라미터 w와 b로 미분을 해보면,(w,b는 각각 시그모이드 함수의 weight값과 bias 값이다)

다음과 같은 결과가 나오고,
계산을 해보면 전자는 0.0043, 후자는 0.0029만큼, Ironical하게도 전자(idx=0)가 더 크게 벌점을 받게 되었다.
즉, 에러가 더 큰 상황에 낮은 벌점을 주더라도, 그레디언트는 오류를 줄이는 방향을 제대로 제공해주므로 최저점을 찾아가
는 데는 문제가 없다. 하지만 학습이 느리게 이루어지고, 이는 심각한 문젯거리이다.
이러한 문제를 MSE 대신에 Cross-Entropy를 사용함으로서 해결할 수가 있다.
교차 엔트로피(Cross-Entropy)
따라서, 딥러닝은 적어도 분류 문제에서는 로스함수로 MSE대신 Cross Entropy를 주로 사용한다.
(위에서 언급한 MSE의 불공평성 문제 때문!! 그러나 [컴퓨터 비전과 딥러닝]의 PG 7-2를 보면 알겠지만, 딥러닝 모델 분류 문제를 MSE로 사용하고 있으므로, 분류 문제를 MSE로 사용한다고 해서 학습이 완전히 안 되는 것은 아니다)
(회귀 모델은 MSE를 사용하는 것이 타당)

여기서 상황을 간단히 하여, y 는 {0, 1}의 값을 가지는 확률변수이고, o가 신경망의 출력 확률변수라고 해보자.
즉, P가 정답 레이블, Q를 신경망 출력에 해당한다고 하면, 교차 엔트로피 목적함수를 쓸 수 있다.

이 목적함수 (loss 함수)가 제구실을 다하는 지 확인해보자.
y = 1, o = 0.98일 때 예측을 꽤나 잘한 것인데, 에러가 0.0291이 되어 매우 낮고,
y = 1, o = 0.0001이라면 예측이 엉터리 인데, 에러가 13.2877나 되어 매우 크다.
(아래를 자세히 읽으면, 에러값이 크게 나오고, 작게 나오고가 매우 의미 있는 결과임을 알 수가 있다)
따라서 목적함수로 매우 적합한 함수라 할 수 있다.
위 loss e를 w와 b에 대해 미분해보자.(w는 sigmoid 함수의 weight값이고, b는 bias 값이다)

미분을 해보면, MSE와는 다르게 에러만으로 그레디언트값이 정해지고 있는 것을 알 수 있다.
즉 에러에 비례하여 가중치를 더 많이 수정하여 더 빠른 속도로 학습이 이루어질 것이다.
위는 클래스가 2개인 경우 {0, 1}인 binary cross entropy 를 보여주었다.
여러 클래스에 해당하는 cartegorical cross entropy의 식은 다음과 같다.
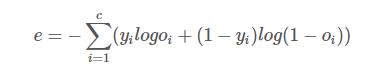
Softmax 활성함수(Activation Function)와 로그우도(Log likelihood) 목적함수
지금까지는 마지막 층 활성화함수로 Sigmoid 함수를 사용하였지만, 마지막 출력 노드의 경우 softmax를 사용하기도 한다.
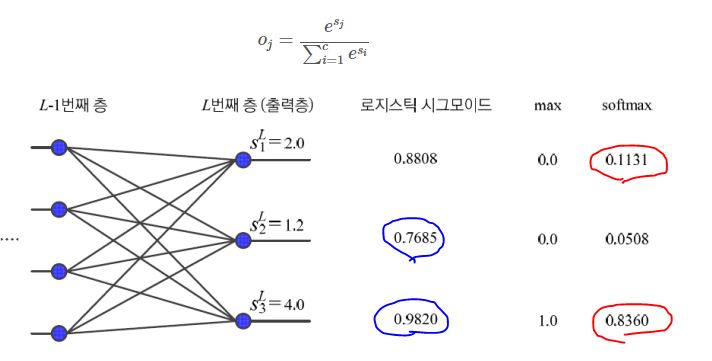
소프트맥스의 장점은 그림에서 보다시피, 최댓값과 최소값의 차이를 극명하게 드러내주어서,
그에 비례하는 가중치로 학습을 시키는 것이다.(정확히는 에러값에 비례하도록 가중치 학습)
softmax 활성화 함수의 짝으로 로그우도를 많이 쓰는데, 식은 다음과 같다.
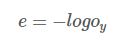
이 목적함수는 모든 노드값을 고려하는 평균제곱 오차나 교차 엔트로피와는 달리, Oy라는 하나의 노드(최대값 노드)값만
본다.
출력값이 1에 근접할 수록 e값은 0에 가까워진다. 즉, 목적함수로써 유용하다.
softmax는 최댓값이 아닌 값을 억제하여 0에 가깝게 만든다는 의도를 가진다.
따라서 학습샘플이 알려주는 부류에 해당하는 출력 노드값만 보겠다는 로그우도 목적함수와 잘 어울린다.
물론 softmax뒤 MSE나 CrossEntropy도 결합해 많이 쓰인다.
어떤 목적함수가 성능이 좋은지 보기위해서는 데이터별 실험하는 것이 최선이다.
(위 글은 아래의 사이트를 참조하였다. https://wordbe.tistory.com/65)


